This page was generated from docs/devices/xylo-imu/configure_preprocessing.ipynb. Interactive online version:

🧑‍🏫 Specifying IMU preprocessing parameters

Xylo™ IMU includes a custom pre-processing and event encoding interface designed to work with IMU data. When designing an IMU signal processing application with Xylo™ IMU, the parameters of the IMU interface should be set appropriately for the given application. This notebook explains the parameters that can be modified by the application developer, and demonstrates how to configure them.

## - Imports and configuration

import numpy as np

# - Plotting and config
import matplotlib.pyplot as plt

plt.rcParams["figure.figsize"] = [9.6, 3.6]
plt.rcParams["figure.dpi"] = 1200
plt.rcParams["font.size"] = 12

try:
    from rich import print
except:
    pass

from IPython.display import Image

import warnings
warnings.filterwarnings('ignore')

from rockpool.devices.xylo.syns63300 import Quantizer

Overview of preprocessing chain modules

Image('imu-ifsim-module.png')

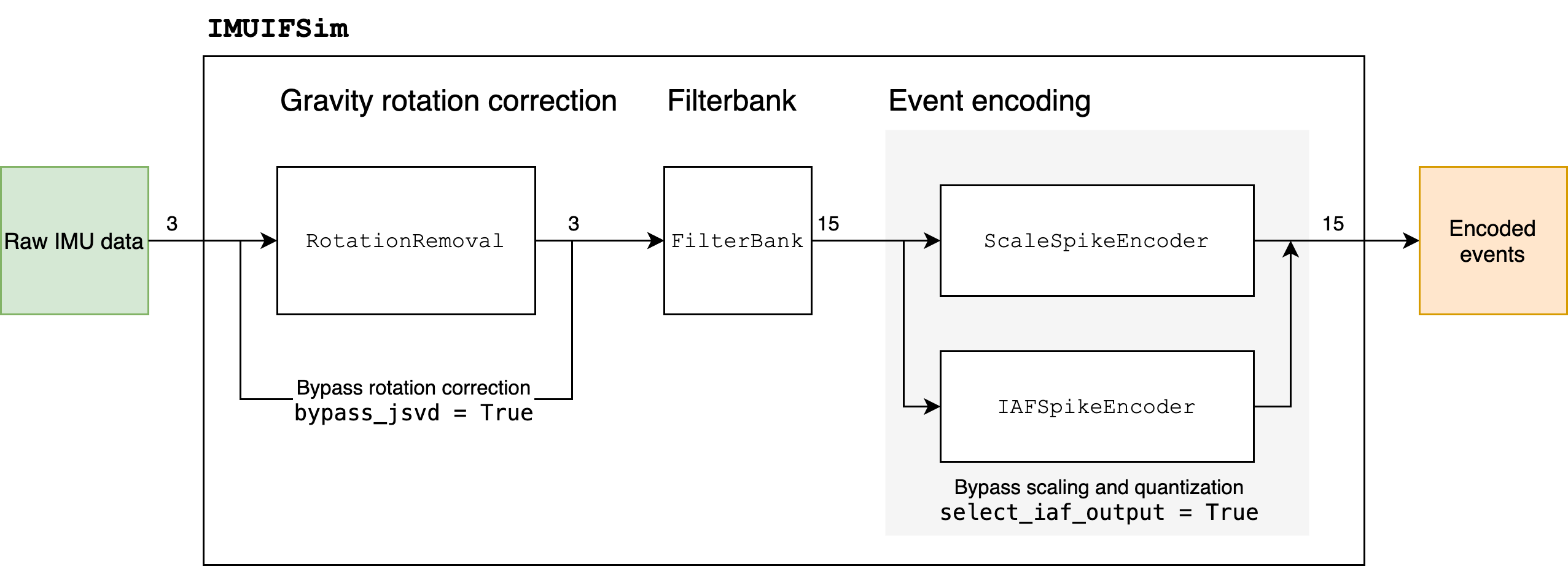
As described in ∿ The Xylo™ IMU preprocessing interface, the IMU IF simulation and configuration is encapsulated in the Rockpool modules RotationRemoval, FilterBank, ScaleSpikeEncoder and IAFSpikeEncoder. This notebook shows how to configure the various logical blocks of the preprocessing chain for desired behaviour.

Specifying rotation correction parameters

The rotation removal block in the IMU interface continuously estimates the sensor orientation in 3-D space, based on the (x, y, z) input signal. This estimation is smoothed over time, with a configurable averaging window for the estimation. It then computes a compensating transformation for the (x, y, z) data which corrects for the sensor orientation, such that the gravity vector is aligned with the -Z axis.

The simulation of this block is embodied by the RotationRemoval class. Only a 3-channel input and 3-channel output shape is supported.

The block offers two configurable parameters:

• Averaging window for estimating the sensor orientation (paramter num_avg_bitshift)

• Sample-and-hold duration determining how often to update the sensor orientation correction (parameter sampling_period)

num_avg_bitshift specifies a low-pass filter smoothing for estimating orientation, with an approximate window length of 2 ** num_avg_bitshift time steps. This paramter defaults to 4 (i.e. 16 time steps).

sampling_period specifies a sample-and-hold duration for the orientation correction, such that the correction information is updated only every sampling_period time steps. This parameter defaults to 10 time steps.

To tune these parameters you should investigate the dynamics of IMU data under your use case. How often and how quickly do you expect a sensor rotation? How important is the information arising from sensor rotation for your application? These aspects will influence how slowly you should correct for sensor rotation, or whether you should do so at all.

from rockpool.devices.xylo.syns63300.imuif import RotationRemoval

rr = RotationRemoval(
    num_avg_bitshift = 6,
    sampling_period = 50,
    )
print(rr)

RotationRemoval  with shape (3, 3) {
    ModSequential 'sub_estimate' with shape (3, 9) {
        SubSpace '0_SubSpace' with shape (3, 9)
        SampleAndHold '1_SampleAndHold' with shape (9, 9)
    }
}

## - Demonstrate using an IMU data sample

# - Load a data sample and ensure it has the correct scale
with open("data.npy", "rb") as f:
    data = np.load(f)
quantizer = Quantizer(3, scale=0.49, num_bits=16)
data_quantized, _, _ = quantizer(data)

# - Apply the rotation removal correction
data_corrected, _, _ = rr(data_quantized)

# - Plot the IMU sample and rotation corrected sample
times = np.arange(len(data)) / 200.
plt.figure()
plt.plot(times, data_quantized[0])
plt.plot(times[[0, -1]], [0, 0], 'k:')
plt.yticks([])
plt.title(f"Quantized IMU Sample Record")
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')

plt.figure()
plt.plot(times, data_corrected[0])
plt.plot(times[[0, -1]], [0, 0], 'k:')
plt.yticks([])
plt.title(f"Rotation Removed IMU Sample Record")
plt.xlabel('Time (s)')
plt.ylabel('Amplitude');

Specifying filter-bank parameters

Specifying a single band-pass filter

The classes FilterBank and BandPassFilter are used to specify and simulate a bank of filters for IMU data. Individual filters are specified by providing a low-pass and high-cut frequency, as well as a sampling frequency.

On Xylo IMU, data is designed to be sampled at 200~Hz.

Here we will show how to specify a band-pass filter with a pass-band between 5 and 10 Hz, at the default sampling frequency of 200 Hz. In the code below we specify the sampling frequency explicitly, but to use the default on Xylo™ IMU you can skip this argument.

from rockpool.devices.xylo.syns63300.imuif import FilterBank, BandPassFilter

# - Specify a band-pass from 5..10 Hz, sampling at 200 Hz
low_cut = 5. # Hz
high_cut = 10. # Hz
Fs = 200. # Hz

# - Instantiate an object for the band-pass filter
bpf = BandPassFilter.from_specification(low_cut, high_cut, Fs)
print(bpf)

BandPassFilter(B_b=3, B_wf=8, B_af=12, a1=-59258, a2=27986, scale_out=0.5836772581461334)

Warning

Note that BandPassFilter is not a Rockpool module, but simply a utility class simulating filters.

We can investigate the transfer response of the filter by showing the result of filtering a chirp signal. To accomplish this we use the chirp() function from scipy.signal. We pass the linear chirp through the single band-pass filter twice, to remove any filter onset transients. We then plot the chirp response and estimate the filter power spectrum.

## - Generate and plot a chirp response

# - Import utility functions
import numpy as np
import scipy.signal as sig

# - Generate a 10-second chirp signal ranging 40..0..40 Hz
T = 5.
times = np.arange(0, int(T * Fs)) / Fs
chirp = np.array(sig.chirp(times, 0, T, 40) * 100, dtype=np.int64).astype(object)
freq = np.linspace(0, 40, len(times))

times2 = np.concatenate([times, times + times[-1]+1/Fs])
chirp2 = np.concatenate([chirp, np.flip(chirp)])
freq2 = np.concatenate([freq, np.flip(freq)])

# - Pass the signal through the filter
resp = bpf(chirp2)

# - Plot the chirp and the filter response
plt.figure()
plt.plot(times, chirp, label = 'Chirp')
plt.plot(times, np.flip(resp[len(times)-1:-1]), label = 'Response')
plt.legend()
plt.title('Filter chirp response')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude');

## - Compute and plot a power spectrum

# - Compute a response power spectrum
hist, fbins, abins = np.histogram2d(freq, np.flip(resp[len(times)-1:-1]) ** 2, 60)
f_ind, a_ind = np.where(hist)

# - Plot the plower spectrum
plt.scatter(fbins[f_ind], abins[a_ind], label = 'Power spectrum')
plt.plot([low_cut, low_cut], abins[[0, -1]], 'r--', label = 'Low cut')
plt.plot([high_cut, high_cut], abins[[0, -1]], 'g--', label = 'High cut')
plt.legend()
plt.yticks([])
plt.title('Filter response power spectrum')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Power');

Specifying parameters for a whole filter-bank

Specifying the parameters for an entire filter-bank requires to specify the size of the filter-bank, as well as the low- and high-cut parameters for each of the filters. Here we will demonstrate by building a filter-bank with one input channel and three band-pass filters.

# - Specify a filterbank and pass the previous chirp signal through
fb = FilterBank.from_specification(3, (0.1, 5), (10, 20), (20, 40))
resp_fb, _, _ = fb(chirp2)

## - Plot the chirp response and frequency power spectra

# - Plot the filter-bank response
plt.figure()
plt.plot(times, np.flip(resp_fb[0, len(times)-1:-1], axis=0), label = ['0.1--5Hz', '10--20Hz', '20--40Hz'])
plt.legend()
plt.title('Filter chirp response')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude');

# - Compute a response power spectrum
hist0, _, _ = np.histogram2d(freq, np.flip(resp_fb[0, len(times)-1:-1, 0]) ** 2, [fbins, abins])
hist1, _, _ = np.histogram2d(freq, np.flip(resp_fb[0, len(times)-1:-1, 1]) ** 2, [fbins, abins])
hist2, _, _ = np.histogram2d(freq, np.flip(resp_fb[0, len(times)-1:-1, 2]) ** 2, [fbins, abins])

f_ind0, a_ind0 = np.where(hist0)
f_ind1, a_ind1 = np.where(hist1)
f_ind2, a_ind2 = np.where(hist2)

# - Plot the plower spectrum
plt.figure()
plt.scatter(fbins[f_ind0], abins[a_ind0], label = '0.1--5Hz')
plt.scatter(fbins[f_ind1], abins[a_ind1], label = '10--20Hz')
plt.scatter(fbins[f_ind2], abins[a_ind2], label = '20--40Hz')
plt.legend()
plt.yticks([])
plt.title('Filter response power spectrum')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Power');

Applying a filterbank to an IMU signal

We can now generate a default filterbank for Xylo IMU, and apply it to the rotation-corrected data from above.

# - Generate a default filterbank
fb = FilterBank()

# - Apply the filterbank to the IMU data
filtered_imu, _, _ = fb(data_corrected)

# - Plot the filter channel outputs
times = np.arange(len(data)) / 200.
plt.plot(times, filtered_imu[0])
plt.title('Filtered signal')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude');

Specifying event encoding method and parameters

Two methods for event encoding are available on Xylo™ IMU:

• Scale and quantise the direct filter bank output channels to up to 15 events per time step, simulated with the module ScaleSpikeEncoder

• Use an integer integrate-and-fire spiking neuron for each channel, with up to 1 event per time step, simulated with the module IAFSpikeEncoder

Configuring the scale-and-quantise approach

The ScaleSpikeEncoder module rectifies the input signal, down-scales the input with a configurable right-shift (num_scale_bits), then truncates the result to num_out_bits == 4 bits.

The only configurable parameter is num_scale_bits, which is 5 by default.

## - Demonstrate the effect of `ScaleSpikeEncoder`

from rockpool.devices.xylo.syns63300.imuif import ScaleSpikeEncoder

scale_encoder = ScaleSpikeEncoder(num_scale_bits=7)
scaled, _, _ = scale_encoder(filtered_imu)

plt.imshow(scaled[0].astype(float).T, aspect='auto', origin='lower', interpolation='none')
xticks, _ = plt.xticks()
xlim = plt.xlim()
plt.xticks(xticks, xticks / Fs)
plt.xlim(xlim)
plt.xlabel('Time (s)')
plt.ylabel('Channel')
plt.title('Quantised encoded IMU signal');

Configuring the Integrate-And-Fire encoder

The IAFSpikeEncoder module sums the absolute input over time, then emits a spike whenever the cumulated value passes a configurable threshold. The neuron state value is then reset by subtracting threshold, and the integration continues.

The only configurable parameter for IAFSpikeEncoder is the threshold parameter, which may adopt values 0..2**31. The default threshold is 1024 for all neurons.

## - Demonstrate the IAF spike encoder
from rockpool.devices.xylo.syns63300.imuif import IAFSpikeEncoder

iaf_encoder = IAFSpikeEncoder(threshold = 1024)
encoded, _, _ = iaf_encoder(filtered_imu)

plt.imshow(encoded[0].astype(float).T, aspect='auto', origin='lower', interpolation='none')
xticks, _ = plt.xticks()
xlim = plt.xlim()
plt.xticks(xticks, xticks / Fs)
plt.xlim(xlim)
plt.xlabel('Time (s)')
plt.ylabel('Channel')
plt.title('IAF encoded IMU signal');

Putting it all together

To configure the IMUIFSim module, you can specify the individual tunable parameters for each of the block elements described above, as well as by using the boolean flags to select or bypass the configurable elements.

IMUIFSim(
    shape: Tuple = (3, 15),

    ## - Sampling frequency used by the IMU interface
    sampling_freq: float = 200.,

    ## - Bypass the rotation correction
    bypass_jsvd: bool = False,

    ## - Rotation correction arguments
    num_avg_bitshift: int = 4,
    SAH_period: int = 10,

    ## - Define the band-pass filters
    filter_list: List = (Default filter list),

    # - Use IAF or ScaleAndQuantize encoder
    select_iaf_output: bool = False,

    ## - ScaleAndQuantize arguments
    scale_values: List[int] = 5,

    ## - IAFEncoder arguments
    iaf_threshold_values: List[int] = 1024,
)

## - Instantiate and demonstrate the IMUIF module

from rockpool.devices.xylo.syns63300 import IMUIFSim

# - Instantiate the IMU IF simulation module
imuif = IMUIFSim()

# - Apply the module to the IMU sample data
encoded, _, _ = imuif(data_quantized)

# - Plot the result
plt.imshow(encoded[0].astype(float).T, aspect = 'auto', interpolation = 'none', origin = 'lower')
xticks, _ = plt.xticks()
xlim = plt.xlim()
plt.xticks(xticks, xticks / Fs)
plt.xlim(xlim)
plt.xlabel('Time (s)')
plt.ylabel('Channel')
plt.title('Encoded IMU signal');