This page was generated from docs/basics/time_series.ipynb. Interactive online version:

Working with time series data

Concepts

In Rockpool, temporal data (“time series” data) is encapsulated in a set of classes that derive from TimeSeries. Time series come in two basic flavours: “continuous” time series, which have been sampled at some set of time points but which represent values that can exist at any point in time; and “event” time series, which consist of discrete event times.

The TimeSeries subclasses provide methods for extracting, resampling, shifting, trimming and manipulating time series data in a convenient fashion. Since Rockpool naturally deals with temporal dynamics and temporal data, TimeSeries objects are used to pass around time series data both as input and as output.

TimeSeries objects have an implicit shared time-base at \(t_0 = 0\) sec. However, they can easily be offset in time, concatenated, etc.

Housekeeping and import statements

# - Import required modules and configure

# - Switch off warnings
import warnings

warnings.filterwarnings("ignore")

# - Required imports
import numpy as np

from rockpool.timeseries import (
    TimeSeries,
    TSContinuous,
    TSEvent,
    set_global_ts_plotting_backend,
)

from IPython.display import Image

# - Use HoloViews for plotting
import sys
!{sys.executable} -m pip install --quiet colorcet holoviews
import colorcet as cc
import holoviews as hv

hv.extension("bokeh")

%opts Curve [width=600]
%opts Scatter [width=600]

Continuous time series represented by TSContinuous

Continuous time series are represented by tuples \([t_{k}, a(t_{k})]\), where \(a(t_{k})\) is the amplitude of a signal, sampled at the time \(t_{k}\). A full time series is therefore the set of samples \([t_{k}, a(t_{k})]\) for \(k=1\dots K\).

Continuous time series in Rockpool are represented by the TSContinuous class.

A time series is constructed by providing the sample times in seconds and the corresponding sample values. The full syntax for constructing a TSContinuous object is given by

def __init__(
    self,
    times: Optional[ArrayLike] = None,
    samples: Optional[ArrayLike] = None,
    num_channels: Optional[int] = None,
    periodic: bool = False,
    t_start: Optional[float] = None,
    t_stop: Optional[float] = None,
    name: str = "unnamed",
    interp_kind: str = "linear",
)

# - Build a time trace vector
duration = 10.0
dt = 0.01
times = np.arange(0.0, duration, 0.1)
theta = times / duration * 2 * np.pi

# - Create a TSContinuous object containing a sin-wave time series
ts_sin = TSContinuous(
    times=times,
    samples=np.sin(theta),
    name="sine wave",
)
ts_sin

non-periodic TSContinuous object `sine wave` from t=0.0 to 9.9. Samples: 100. Channels: 1

TSContinuous provides a convenience method from_clocked() to generate a TSContinuous object from a regularly-sampled vector of data with a fixed time-step dt. This is the optimal way to work with clocked data imported from outside Rockpool, and ensures that the data will be used intuitively within Rockpool.

from_clocked() will return a TSContinuous time series with extent from t = 0 to t = N * dt, using sample-and-hold interpolation between samples. Each data sample is assumed to occur at the beginning of a time bin of dt duration, and the data is assumed to be valid for the entirity of the dt time bin.

You can offset the returned time series accurately by specifying the time of the initial sample with the argument t_start.

# - Generate some data samples
N = 100
dt = 0.01
samples = np.random.rand(N, 1)

ts_reg = TSContinuous.from_clocked(samples, dt=dt, t_start=5.0)
ts_reg

non-periodic TSContinuous object `unnamed` from t=5.0 to 6.0. Samples: 100. Channels: 1

TSContinuous objects provide a convenience plotting method plot() for visualisation. This makes use of holoviews / bokeh or matplotlib plotting libraries, if available.

If both are available you can choose between them using the timeseries.set_global_plotting_backend function.

# - Set backend for Timeseries to holoviews
set_global_ts_plotting_backend("holoviews")

# # - Alternatively, it can be set for specific Timeseries instances
# ts_sin.set_plotting_backend("holoviews")

# - Plot the time series
ts_sin.plot()

Global plotting backend has been set to holoviews.

TSContinuous objects can represent multiple series simultaneously, as long as they share a common time base:

# - Create a time series containing a sin and cos trace
ts_cos_sin = TSContinuous(
    times=times,
    samples=np.stack((np.sin(theta), np.cos(theta))).T,
    name="sine and cosine",
)
# - Print the representation
print(ts_cos_sin)

# - Plot the time series`
ts_cos_sin.plot()

non-periodic TSContinuous object `sine and cosine` from t=0.0 to 9.9. Samples: 100. Channels: 2

For convenience, TimeSeries objects can be made to be periodic. This is particularly useful when simulating networks over repeated trials. To do so, use the periodic flag when constructing the TimeSeries object:

# - Create a periodic time series object
ts_sin_periodic = TSContinuous(
    times=times,
    samples=np.sin(theta),
    periodic=True,
    name="periodic sine wave",
)
# - Print the representation
print(ts_sin_periodic)

# - Plot the time series
plot_trace = np.arange(0, 100, dt)
ts_sin_periodic.plot(plot_trace)

periodic TSContinuous object `periodic sine wave` from t=0.0 to 9.9. Samples: 100. Channels: 1

Continuous time series permit interpolation between sampling points, using scipy.interpolate as a back-end. By default sample-and-hold interpolation is used, but any interpolation method supported by scipy.interpolate can be provided as a string when constructing the TSContinuous object (for example, linear).

The interpolation interface is simple: TSContinuous objects are callable with a list-like set of time points; the interpolated values at those time points are returned as a numpy.ndarray.

# - Interpolate the sine wave
print(ts_sin([1, 1.1, 1.2]))

[[0.58778525]
 [0.63742399]
 [0.63742399]]

As a convenience, TSContinuous objects can also be indexed using [], which uses interpolation to build a new time series object with the requested data. A second index can be provided to choose specific channels. Indexing will return a new TSContinuous object.

# - Slice a time series object
ts_cos_sin[:1:0.09, 0].print()

non-periodic TSContinuous object `sine and cosine` from t=0.0 to 0.99. Samples: 12. Channels: 1
0.0:     [0.]
0.09:    [0.]
0.18:    [0.06279052]
0.27:    [0.12533323]
        ...
0.72:    [0.42577929]
0.8099999999999999:      [0.48175367]
0.8999999999999999:      [0.48175367]
0.99:    [0.53582679]

For non-periodic TSContinuous objects, the time range in which data can be sampled or interpolated lies between the earliest and the latest sample or, in other words, between the first and last point of its times attribute. It is possible that the limits of the time series, which are defined by the t_start and t_stop attributes, are beyond the sampling times. In this case values in the corresponding intervals are determined by the fill_value attribute. The default behavior is to extrapolate.

# - Extrapolate between last sample and t_stop
ts_cos_sin.t_stop = 12
print("Extrapolated fill value at t=11:", ts_cos_sin(11))

# - Use constant fill value instead of extrapolation
ts_cos_sin.fill_value = 42
print("New fill value at t=11:", ts_cos_sin(11))

# - Back to extrapolation
ts_cos_sin.fill_value = "extrapolate"

Extrapolated fill value at t=11: [[-0.06279052  0.99802673]]
New fill value at t=11: [[42. 42.]]

When trying to sample outside of this range, the default behavior is to raise a ValueError:

# - Sampling at a point beyond the series' time range:
try:
    ts_cos_sin(13)
except ValueError as e:
    print("Caught the following exception:")
    print(e)

Caught the following exception:
TSContinuous `sine and cosine`: Some of the requested time points are beyond the first and last time points of this series and cannot be sampled.
If you think that this is due to rounding errors, try setting the `approx_limit_times` attribute to `True`.
If you want to sample at these time points anyway, you can set the `beyond_range_exception` attribute of this time series to `False` and will receive `NaN` as values.

If the beyond_range_exception attribute is set to False, nan values will instead be returned and a warning will be issued. (You will not see the warning here, because warnings are suppressed in this tutorial)

ts_cos_sin.beyond_range_exception = False
print(ts_cos_sin(13))

[[nan nan]]

Sometimes it can happen due to numerical errors that the provided sampling time is slightly beyond range, although the intention may have been to sample right at the beginning or end of a time series. This will result in a ValueError or nan values being returned, depending on the value of beyond_range_exception . However, when the approx_limit_times attribute is set to True (the default case), values that are only slightly beyond the defined range will be approximated by the first or last time point of the series. For a time series with approx_limit_times set to True, the threshold for this approximation is 1e-6 * ts.duration or 1e-9, whichever is less. In either case a warning will be raised.

# - `t` should be 12, but is slightly larger due to numerical errors.
times = np.repeat(0.001, 12000)
t = np.sum(times)
print(
    f"We want to sample about {t - ts_cos_sin.t_stop:.1e} seconds after the series ends."
)

# - Sampling at `t` will give same value as if sampled at t=12
print("Sampling in spite of rounding errors:", ts_cos_sin(t))
print("Values at end of series:", ts_cos_sin(12))

We want to sample about 5.3e-15 seconds after the series ends.
Sampling in spite of rounding errors: [[-0.06279052  0.99802673]]
Values at end of series: [[-0.06279052  0.99802673]]

# - Disable time approximation in such cases
ts_cos_sin.approx_limit_times = False

# - Sampling at `t` will result in a warning and nan-values being returned.
print("Now we get:", ts_cos_sin(t))

Now we get: [[nan nan]]

TSContinuous provides a large number of methods for manipulating time series. For example, binary operations such as addition, multiplication etc. are supported between two time series as well as between time series and scalars. Most operations return a new TSContinuous object.

See the api reference for TSContinuous for full detail.

Attributes (TSContinuous)

Attribute name	Description
times	Vector \(T\) of sample times
samples	Matrix \(T\times N\) of samples, corresponding to sample times in times
num_channels	Scalar reporting \(N\): number of series in this object
num_traces	Synonym to num_channels
t_start, t_stop	First and last sample times, respectively
duration	Duration between t_start and t_stop
plotting_backend	Current plotting backend for this instance.
fill_value	Data to use to fill samples that fall outside t_start and t_stop

Examples of time series manipulation

# - Perform additions, powers and subtractions of time series
ts_sin.beyond_range_exception = False
(
    (ts_sin + 2).plot()
    + (ts_cos_sin**6).plot()
    + (ts_sin - (ts_sin**3).delay(2)).plot()
).cols(1)

Event-based time series represented by TSEvent

Sequences of events (e.g. spike trains) are represented by the TSEvent class, which inherits from TimeSeries.

Discrete time series are represented by tuples \((t_k, c_k)\), where \(t_k\) are sample times as before and \(c_k\) is a “channel” associated with each sample (e.g. the source of an event).

Multiple samples at identical time points are explictly permitted such that (for example) multiple neurons could spike simultaneously.

Unless the series is empty, the argument t_stop must be provided and has to be strictly larger than the time of the last event.

TSEvent objects are initialised with the syntax

def __init__(
    self,
    times: ArrayLike = None,
    channels: Union[int, ArrayLike] = None,
    periodic: bool = False,
    t_start: Optional[float] = None,
    t_stop: Optional[float] = None,
    name: str = None,
    num_channels: int = None,
)

# - Build a time trace vector
times = np.sort(np.random.rand(100))
channels = np.random.randint(0, 10, (100))
ts_spikes = TSEvent(
    times=times,
    channels=channels,
    t_stop=100,
)
ts_spikes

non-periodic `TSEvent` object `unnamed` from t=0.001941216549281144 to 100.0. Channels: 10. Events: 100

# - Plot the events
ts_spikes.plot()

If TSEvent is called, it returns arrays of the event times and channels that fall within the defined time points and correspond to selected channels.

# - Return events between t=0.5 and t=0.6
ts_spikes(0.5, 0.6)
ts_spikes(0.5, 0.6, channels=[3, 7, 8])

(array([0.51589083, 0.58430924, 0.59280105]), array([3, 8, 7]))

TSEvent also supports indexing, where indices correspond to the indices of the events in the times attribute. A new TSEvent will be returned. For example, in order to get a new series with the first 5 events of ts_spikes one can do:

ts_spikes[:5]

non-periodic `TSEvent` object `unnamed` from t=0.001941216549281144 to 100.0. Channels: 10. Events: 5

TSEvent provides several methods for combining multiple TSEvent objects and for extracting data. See the API reference for TSEvent for full details.

Attributes (TSEvent)

Attribute name	Description
times	Vector \(T\) of sample times
channels	Vector of channels corresponding to sample times in times
num_channels	Scalar \(C\): number of channels in this object
t_start, t_stop	First and last sample times, respectively
duration	Duration between t_start and t_stop
plotting_backend	Current plotting backend for this instance.

Importing time series data

Time series data imported from outside Rockpool often comes in a “clocked” format, where the data is presented as a vector of samples on an implicit time base. Sample times are often on a fixed clock dt or sample frequency fs = 1 / dt.

These representations can easily be imported into Rockpool, but some care is required to make sure the data is handled correctly.

For continuous-time data, TSContinuous provides the method from_clocked().

def TSContinuous.from_clocked(
    samples: numpy.ndarray,
    dt: float,
    t_start: float = 0.0,
    periodic: bool = False,
    name: str = None,
) -> TSContinuous

This method will accept regularly sampled data on a specified sample clock dt, from multiple channels, and will return a correctly-formatted TSContinuous object with extents set correctly. This object will use “sample-and-hold” interpolation, as this seems to be the most common mental model that developers have for data resampled within a time bin.

# - Get a data sample
T = 100
C = 3
dt = 0.1
data = np.random.rand(T, C)

# - Create the time series
ts = TSContinuous.from_clocked(data, dt=dt)
print(ts)

non-periodic TSContinuous object `unnamed` from t=0.0 to 10.0. Samples: 100. Channels: 3

Similarly, imported event data often appears in a “raster” format, which is regularly clocked. In this format, a train of events on \(C\) channels over \(T\) time bins is represented as a matrix \((T, C)\), where the element \((t, c)\) indicates the number of events occurring during integer time bin \(t\) on channel \(c\).

In the example below, seven channels emit events over seven time bins. We will use the TSEvent.from_raster() method to convert the set of events from a numpy.ndarray into a TSEvent object. This will ensure that t_start, t_stop and num_channels attributes are set approprately.

def from_raster(
    raster: np.ndarray,
    dt: float = 1.0,
    t_start: float = 0.0,
    t_stop: Optional[float] = None,
    name: Optional[str] = None,
    periodic: bool = False,
    num_channels: Optional[int] = None,
    spikes_at_bin_start: bool = False,
) -> TSEvent:

Image("raster_to_TSEvent.png")

Note that the events are placed in the middle of each time bin. This behaviour can be modifed with the spikes_at_bin_start argument to TSEvent.from_raster().

# - Generate a boolean raster
T = 10
C = 20
rate = 0.1
raster = np.random.rand(T, C) <= 0.1

# - Convert to a time series using `.from_raster()`
ts = TSEvent.from_raster(raster)
print(ts)
ts.plot()

non-periodic `TSEvent` object `unnamed` from t=0.0 to 10.0. Channels: 20. Events: 28

Time series internal representation

TSContinuous internal representation

Continuous-valued time series, represented by TSContinuous, are stored internally as a vector of sample times times with shape \((T, 1)\), and a corresponding matrix of samples samples with shape \((T, C)\) (where \(C\) is the number of channels in the time series. This implies that all series stored within a single TSContinuous object are sampled on the same time base. By convention, samples are always stored in time-sorted order.

Note that times does not need to be on a regular clock; each sample time is independent. For example, we can generate the time series:

times = [2, 3, 5, 7.5, 8, 10.25]
samples = [[2, 11.5], [6, 11], [5, 7], [2.5, 8.5], [3.5, 12.5], [10.5, 11]]

ts = TSContinuous(times, samples, interp_kind="linear")
print(ts)
print(".times:", ts.times)
print(".samples:\n", ts.samples)

non-periodic TSContinuous object `unnamed` from t=2.0 to 10.25. Samples: 6. Channels: 2
.times: [ 2.    3.    5.    7.5   8.   10.25]
.samples:
 [[ 2.  11.5]
 [ 6.  11. ]
 [ 5.   7. ]
 [ 2.5  8.5]
 [ 3.5 12.5]
 [10.5 11. ]]

Image(filename="continuous-representation.png")

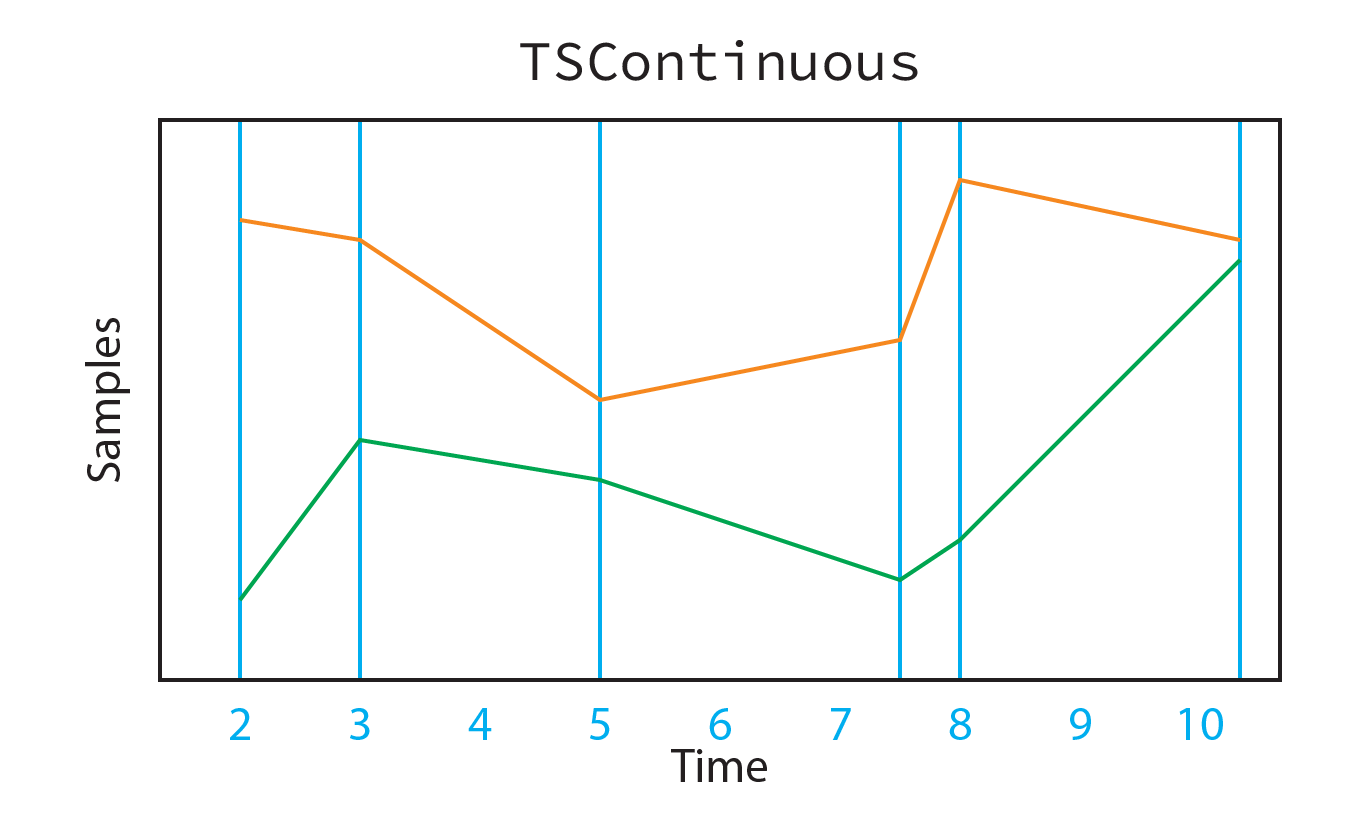
If you need a clocked representation for some reason, then you should generate a time base and interpolate the samples:

ts

non-periodic TSContinuous object `unnamed` from t=2.0 to 10.25. Samples: 6. Channels: 2

dt = 0.75
time_base = np.arange(15) * dt
ts.beyond_range_exception = False
samples = ts(time_base)
print("time_base:", time_base)
print("samples:\n", samples)

time_base: [ 0.    0.75  1.5   2.25  3.    3.75  4.5   5.25  6.    6.75  7.5   8.25
  9.    9.75 10.5 ]
samples:
 [[        nan         nan]
 [        nan         nan]
 [        nan         nan]
 [ 3.         11.375     ]
 [ 6.         11.        ]
 [ 5.625       9.5       ]
 [ 5.25        8.        ]
 [ 4.75        7.15      ]
 [ 4.          7.6       ]
 [ 3.25        8.05      ]
 [ 2.5         8.5       ]
 [ 4.27777778 12.33333333]
 [ 6.61111111 11.83333333]
 [ 8.94444444 11.33333333]
 [        nan         nan]]

Note that some samples are nan — this is because TSContinuous objects do not allow extrapolation beyond the bounds of the time series, defined by t_start and t_stop. By default, a ValueError would been thrown if beyond_range_exception had not been set to False.

TSEvent internal representation

TSEvent objects have a different internal representation. They contain a vector times of length \(N\) samples, defining points in time when an event occurs; and a corresponding vector channels of length \(N\), containing the integer channels corresponding to each sample in times.

times = [0.2, 0.8, 1.2, 1.4, 1.8, 2.2, 3.3, 3.5, 3.6, 4.2, 4.8, 5.2, 5.8, 6.2, 6.5, 6.8]
channels = [0, 3, 3, 1, 6, 6, 3, 3, 5, 5, 4, 0, 5, 1, 1, 2]
ts = TSEvent(times, channels, t_start=0.0, t_stop=7.0)

print(".times:", ts.times)
print(".channels:", ts.channels)
ts.plot();

.times: [0.2 0.8 1.2 1.4 1.8 2.2 3.3 3.5 3.6 4.2 4.8 5.2 5.8 6.2 6.5 6.8]
.channels: [0 3 3 1 6 6 3 3 5 5 4 0 5 1 1 2]

You may need to export the TSEvent object as an event raster; a common clocked event representation, where time is discretised into bins of fixed duration dt. To do this, TSEvent provides the method raster().

def raster(
    dt: float,
    t_start: float=None,
    t_stop: float=None,
    num_timesteps: int=None,
    channels: numpy.ndarray=None,
    add_events: bool=False,
    include_t_stop: bool=False,
) -> numpy.ndarray:

ts.raster(dt=0.5)

array([[ True, False, False, False, False, False, False],
       [False, False, False,  True, False, False, False],
       [False,  True, False,  True, False, False, False],
       [False, False, False, False, False, False,  True],
       [False, False, False, False, False, False,  True],
       [False, False, False, False, False, False, False],
       [False, False, False,  True, False, False, False],
       [False, False, False,  True, False,  True, False],
       [False, False, False, False, False,  True, False],
       [False, False, False, False,  True, False, False],
       [ True, False, False, False, False, False, False],
       [False, False, False, False, False,  True, False],
       [False,  True, False, False, False, False, False],
       [False,  True,  True, False, False, False, False]])

The conversion is illustrated below for this event time series, and dt = 1.0. In this case, since multiple events can occur within one dt, we use the argument add_events = True.

def raster(
    self,
    dt: float,
    t_start: float = None,
    t_stop: float = None,
    num_timesteps: int = None,
    channels: np.ndarray = None,
    add_events: bool = False,
    include_t_stop: bool = False,
) -> np.ndarray:

# - Rasterise the time series, with a time step of `dt = 1.`
ts.raster(dt=1.0, add_events=True);

Image("TSEvent_to_raster.png")