This page was generated from docs/advanced/graph_overview.ipynb. Interactive online version:

Computational graphs in Rockpool

Graphs is Rockpool are used to convert the structure of an arbitrary network to deploy on neuromorphic hardware. The graphs cannot be used for simulation, and are generally more constrained than networks used for training and simulation.

# - Switch off warnings
import warnings

warnings.filterwarnings("ignore")

Graph base classes

Graphs consist of modules (derived from the class graph.GraphModule), connected over nodes (derived from the class graph.GraphNode).

graph.GraphModule s are units of computation. For example, a set of linear weights; a population of spiking neurons.

graph.GraphModule s contain links to sets of input nodes and output nodes, which define the channels of information flowing in and out of a module. These nodes are graph.GraphNode objects.

from IPython.display import Image
from pathlib import Path

Image(Path("images", "GraphModule.png"))

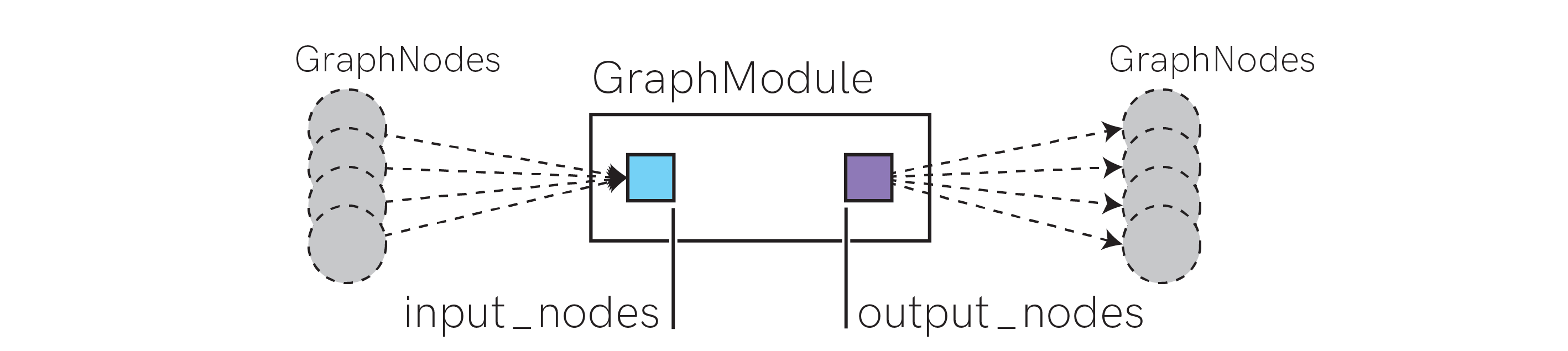
The figure above shows the conceptual contents of a graph.GraphModule. input_nodes and output_nodes are ordered lists containing references to zero or more graph.GraphNode objects.

graph.GraphModule subclasses define specific computational units. They contain all additional parameters needed to define the configuration of the computational unit. For example, see the graph.LIFNeuronWithSynsRealValue class, which contains the configuration parameters needed to define a standard LIF neuron with exponential synapses.

A graph.GraphNode is an object that holds connections between graph.GraphModule s. Each node can have multiple sources and sinks of information.

Image(Path("images", "GraphNode.png"))

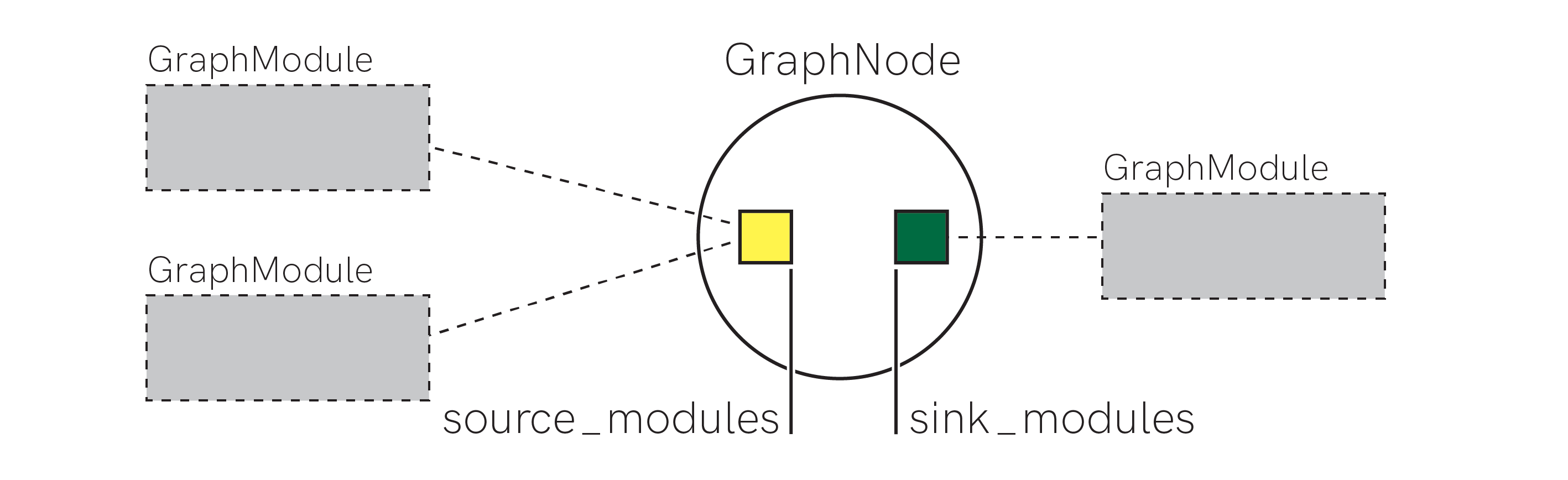
The figure above shows the conceptual contents of a graph.GraphNode object. It simply acts as plumbing between graph.GraphModule objects, holding references to source and sink graph.GraphModule s that are connected over this graph.GraphNode.

Building graphs

You can generate graph.GraphModule s by providing existing input and output nodes explicitly, as well as other parameters. Or you can use the _factory() method, which generates new input and output nodes for the module.

When you instantiate a graph.GraphModule subclass, you can provide additional arguments to the constructor or the _factory() method to fill in extra attributes of the object.

You should connect modules using the graph.utils.connect_modules() function. This function wires up two modules by merging the output nodes from the source module with the input nodes of the destination module.

Image(Path("images", "connect.png"))

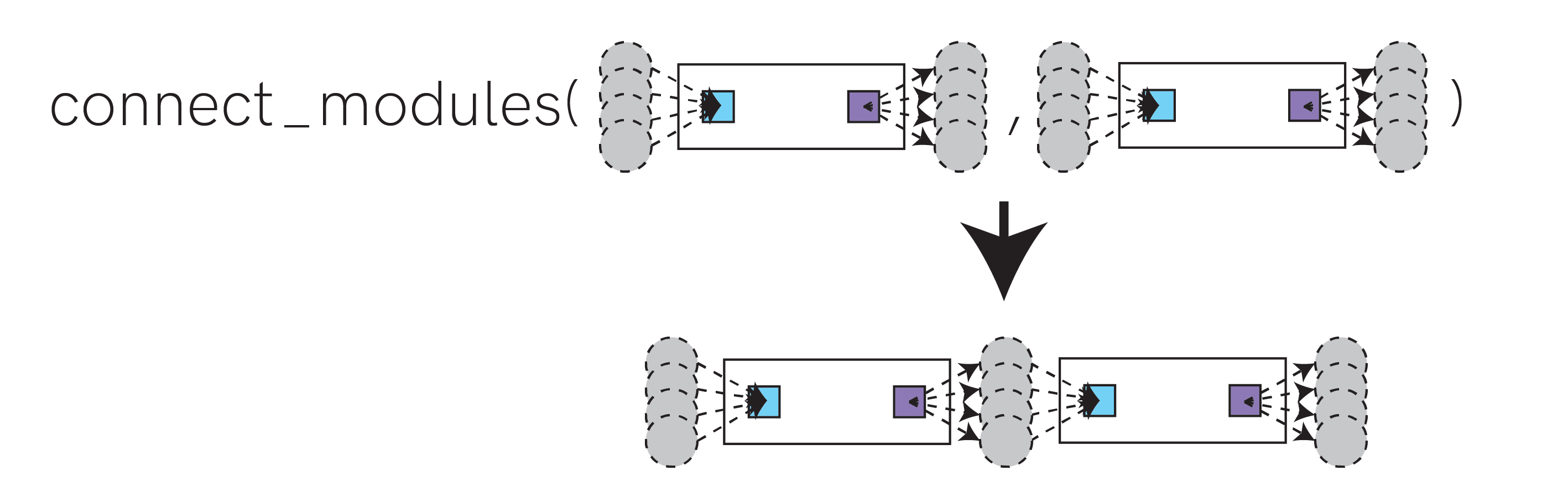
graph.utils.connect_modules() also supports connecting subsets of output / input nodes. See the help for graph.utils.connect_modules() for more details.

Once you have built up a graph, you can can conveniently encapsulate complex graphs and subgraphs using the graph.GraphHolder class.

Image(Path("images", "GraphHolder.png"))

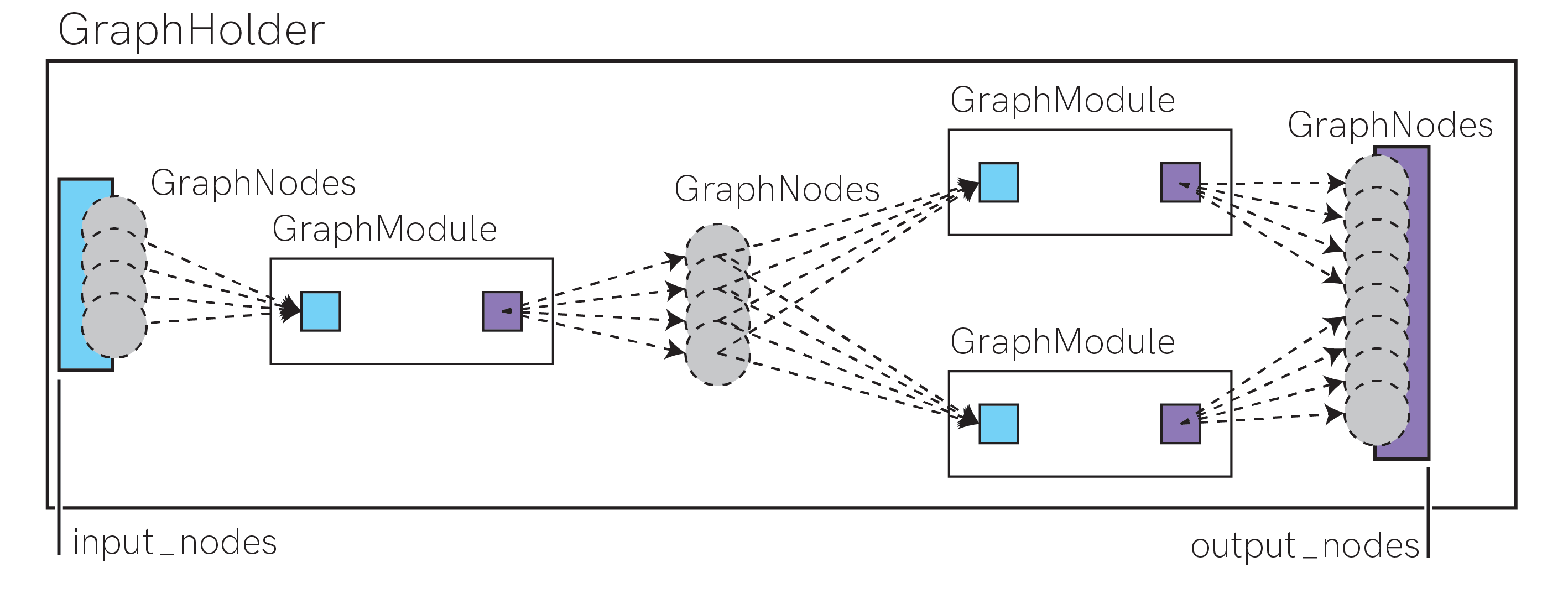
This class only needs the input_nodes and output_nodes arguments, and conceptually holds an entire subgraph linked from those nodes.

You can also use the as_GraphHolder() function to easily encapsulate a GraphModule as a GraphHolder.

Exploring graphs

Graphs can be traversed by iterating over GraphModule.input_nodes, GraphNode.sink_modules, etc.

import rockpool.graph as rg

mod1 = rg.GraphModule._factory(1, 2, "Mod1")
mod2 = rg.GraphModule._factory(2, 1, "Mod2")
rg.connect_modules(mod1, mod2)
graph = rg.GraphHolder(mod1.input_nodes, mod2.output_nodes, "Graph", None)
graph

GraphHolder "Graph" with 1 input nodes -> 1 output nodes

graph.input_nodes[0]

GraphNode 140578474090064 with 0 source modules and 1 sink modules

graph.input_nodes[0].sink_modules[0]

GraphModule "Mod1" with 1 input nodes -> 2 output nodes

graph.input_nodes[0].sink_modules[0].output_nodes[0]

GraphNode 140578474090160 with 1 source modules and 1 sink modules

graph.input_nodes[0].sink_modules[0].output_nodes[0].sink_modules[0]

GraphModule "Mod2" with 2 input nodes -> 1 output nodes

And so on. More convenient traversal and graph search algorithms are provided by the .graph.utils package.

Bags of graphs

graph.utils.bag_graph() converts a graph into two collections: a list of unique GraphModule s in the graph, and a list of unique GraphNode s. It does so by recursively traversing a graph from input to output. Note that any unreachable modules or nodes will not be returned.

rg.bag_graph(graph)

([GraphNode 140578474090064 with 0 source modules and 1 sink modules,
  GraphNode 140578491079408 with 1 source modules and 0 sink modules,
  GraphNode 140578474090160 with 1 source modules and 1 sink modules,
  GraphNode 140578473013152 with 1 source modules and 1 sink modules],
 [GraphModule "Mod1" with 1 input nodes -> 2 output nodes,
  GraphModule "Mod2" with 2 input nodes -> 1 output nodes])

Searching by module class

If you know the specific graph.GraphModule subclass you are looking for, then the helper function graph.utils.find_modules_of_subclass() will be useful. It searches an entire graph for modules of the desired class, and returns a list of unique modules.

import rockpool.graph as rg
import numpy as np

lin = rg.LinearWeights._factory(1, 2, "Lin", None, np.zeros((1, 2)))
rate = rg.RateNeuronWithSynsRealValue._factory(2, 2, "Rate")
rg.connect_modules(lin, rate)
graph = rg.GraphHolder(lin.input_nodes, rate.output_nodes, "Graph", None)

print(rg.find_modules_of_subclass(graph, rg.LinearWeights))
print(rg.find_modules_of_subclass(graph, rg.RateNeuronWithSynsRealValue))

[LinearWeights "Lin" with 1 input nodes -> 2 output nodes]
[RateNeuronWithSynsRealValue "Rate" with 2 input nodes -> 2 output nodes]

Searching for recurrent modules

Loopy graphs are permitted, as are recurrently connected modules. Recurrent modules are GraphModule s where at least two modules are connected back to back (see below)

Image(Path("images", "recurrent_modules.png"))

The helper function graph.utils.find_recurrent_modules() will return any recurrently-connected (in the sense above) GraphModule objects in the graph. Note that it will not return loops with one or more modules in between.

import rockpool.graph as rg

rec_mod1 = rg.GraphModule._factory(2, 2, "Recurrent 1")

# - Use the existing graph nodes to directly connect the two modules recurrently
rec_mod2 = rg.GraphModule(
    rec_mod1.output_nodes,
    rec_mod1.input_nodes,
    "Recurrent 2",
    None,
)
graph = rg.GraphHolder(rec_mod1.input_nodes, rec_mod2.output_nodes, "Graph", None)

rg.find_recurrent_modules(graph)

([GraphModule "Recurrent 2" with 2 input nodes -> 2 output nodes,
  GraphModule "Recurrent 1" with 2 input nodes -> 2 output nodes],
 [GraphModule "Recurrent 2" with 2 input nodes -> 2 output nodes,
  GraphModule "Recurrent 1" with 2 input nodes -> 2 output nodes])

Integrating custom nn.Module s into the computational graph

If you make a custom neuron or custom network architecture, and want that class to participate in the graph extraction API, you need to implement the Module.as_graph() method. This method must return a GraphModule or GraphHolder containing a graph of your module.

Combinators such as ModSequential know how to assemble these sub-graphs into a complete computational graph of the whole network.

Below is an example of a simple custom spiking neuron class that represents itself as an LIF module in the computational graph. It returns an graph.LIFNeuronWithSynsRealValue object, with parameters filled in from the rockpool module.

import rockpool.graph as rg
from rockpool.nn.modules import LIFTorch


class MyLIFNeuron(LIFTorch):
    def as_graph(self) -> rg.GraphModuleBase:
        return rg.LIFNeuronWithSynsRealValue._factory(
            size_in=self.size_in,
            size_out=self.size_out,
            name=self.name,
            computational_module=self,
            tau_mem=self.tau_mem,
            tau_syn=self.tau_syn,
            bias=self.bias,
            dt=self.dt,
        )


mod = MyLIFNeuron(4)
mod.as_graph()

LIFNeuronWithSynsRealValue with 4 input nodes -> 4 output nodes

Other graph module classes that may be useful are LinearWeights, GenericNeurons, AliasConnection and RateNeuronWithSynsRealValue.

More complex network architectures can be encapsulated by GraphHolder objects to return. For example, the below Module subclass contains two submodules — weights and neurons.

from rockpool.nn.modules import Linear, Rate, Module
import rockpool.graph as rg


class WeightedRate(Module):
    def __init__(self, shape: tuple, *args, **kwargs):
        # - Initialise superclass
        super().__init__(shape, *args, **kwargs)

        # - Define two sub-modules
        self.lin = Linear(shape[0:2])
        self.rate = Rate(shape[1])

    def evolve(self, input_data, record: bool = False):
        # - Push data through the sub-modules
        out, ns_lin, rd_lin = self.lin(input_data, record)
        out, ns_rate, rd_rate = self.rate(out, record)

        ns = dict("lin", ns_lin, "rate", ns_rate)
        rd = dict("lin", rd_lin, "rate", rd_rate)

        return out, ns, rd

Now we add a as_graph() override method. This returns a graph that represents the computational graph of this module. The structure of the subgraph must match the computation that takes place in the evolve() method above, since it cannot be extracted automatically.

However, since each sub-module also implements the as_graph() interface, we can quickly and conveniently build a computational graph for our custom module.

class WeightedRate(WeightedRate):
    def as_graph(self) -> rg.GraphModuleBase:
        # - Get a graph module for the two sub-modules
        glin = self.lin.as_graph()
        grate = self.rate.as_graph()

        # - Connnect the two modules
        rg.connect_modules(glin, grate)

        # - Return a graph holder
        return rg.GraphHolder(glin.input_nodes, grate.output_nodes, self.name, self)

mod = WeightedRate((1, 2))
mod.as_graph()

GraphHolder with 1 input nodes -> 2 output nodes

The goal with graphs an sub-graphs is to build a flat structure of computational modules that can be examined programmatically to map the graph onto neuromorphic hardware, or convert its structure.

Next steps

To learn about creating your own mappers onto your own HW, and how to subclass GraphModule, see Graph mapping.