This page was generated from docs/tutorials/adversarial_training.ipynb.
Interactive online version:
👹 Adversarial training
Some computational substrates, for example mixed-signal neuromorphic processors or memristive cross-bar arrays, exhibit device variation from chip to chip and across the surface of a chip. This results in unknown parameter variation when a pre-trained network is deployed onto a chip.
In this tutorial we show how to use the training.adversarial_jax module to train networks that are robust to parameter variation.
This approach is described in more detail in Büchel et al 2021 arXiv: https://arxiv.org/abs/2106.05009 .
Network insensitivity to parameter noise via adversarial regularization
The high-level description of the algorithm is as follows: In each training iteration, the network parameters are attacked by an adversary, whose goal it is to maximize the difference between the network output pre-attack and the network output post-attack. It does so by stepping up the gradient of a loss function \(\mathcal{L}_{rob}(\cdot)\), which takes as arguments the outputs of the network using the attacked parameters and the original parameters. The network evaluation function is given as \(f(X,\Theta)\), for input set \(X\) and parameters \(\Theta\).
This loss function is traditionally chosen as the KL-divergence between the softmaxed logits of both networks. In this tutorial, the MSE was chosen. Note that this function is separate and can be different from the task loss for whatever the network is being trained to do.
The adversary can take a fixed number of steps up the loss gradient, for each training iteration. The size of the steps it can take is also limited, such that the overall attack is described by a “mismatch level”, which is roughly the percentage change in each parameter value that is permitted. e.g. a mismatch level of 10% corresponds to a 10% change of the values in each parameter from the nominal value.
This adversarial attack on the parameters is combined with noise injected into the parameters in each forward pass. Adding parameter noise also improves the robustness of the final network.
For each training iteration, the network optimises a hybrid loss which is a combination of the task loss \(\mathcal{L}_{task}(\cdot)\) and the robustness loss \(\mathcal{L}_{rob}(\cdot)\). By doing so the network learns to solve the task, but in such a way that the network is not badly affected by parameter noise.
The final loss that is being optimized is \(\mathcal{L} = \mathcal{L}_{task}(f(X,\Theta)) + \beta_{rob} \cdot \mathcal{L}_{rob}(f(X,\Theta),f(X,\Theta^*))\), where \(\Theta^*\) are the parameters found by the adversary from the nominal parameters \(\Theta\), and \(\beta_{rob}\) is a hyperparameter that weights the two components of the loss.
The training modules required
Rockpool provides several packages to assist with training Jax-backed models, and to support adversarial training.
The package training.jax_loss provides several useful components for building loss functions, including mean-squared error, KL divergence, softmax and various forms of regularisation.
The package training.adversarial_jax provides functions to perform adversarial attacks on the parameters (pga_attack()), as well as the hybrid loss function \(\\mathcal{L}\) (adversarial_loss()).
adversarial_loss() has the calling signature
def adversarial_loss(
parameters: Tree,
net: JaxModule,
inputs: np.ndarray,
target: np.ndarray,
task_loss: Callable[[np.ndarray, np.ndarray], float],
mismatch_loss: Callable[[np.ndarray, np.ndarray], float],
rng_key: JaxRNGKey,
noisy_forward_std: float = 0.0,
initial_std: float = 1e-3,
mismatch_level: float = 0.025,
beta_robustness: float = 0.25,
attack_steps: int = 10,
) -> float:
This is a compilable, differentiable loss function based on Jax, that evaluates a network net on the parameters parameters (\(\Theta\)), over input with the desired output target. Internally it evaluates the hybrid loss \(\mathcal{L}\) described above, by performing the adversarial attack.
You can supply arbitrary utility loss functions task_loss() (\(\mathcal{L}_{task}\)) and mismatch_loss() (\(\mathcal{L}_{rob}\)) to measure the network performance during training. These apply to the task performance (task_loss()) and provide the metric used by the adversarial attack (mismatch_loss()). These must be based on Jax to support automatic differentiation.
noisy_forward_std provides a way to add Gaussian noise to each parameter during the forward pass through the network. This encourages additional robustness to parameter variation. Keep this at 0.0 if you don’t want to use forward noise.
initial_std is the amount of Gaussian noise added to the nominal parameters to initialise the parameters used by the adversary, as it starts its attack.
mismatch_level is a number > 0 which defines the maximum attack size the adversary is permitted to use. 1.0 means an attack size that is 100% of the parameter scale.
beta_robustness is the weighting hyper-parameter \(\beta_{rob}\), as described above.
attack_steps is the number of gradient-ascent steps taken by the adversary during its attack.
[1]:
# - Useful imports
import warnings
warnings.filterwarnings("ignore")
from jax import config
config.FLAGS.jax_log_compiles = False
config.update("jax_disable_jit", False)
# - Import the adversarial training packages
from rockpool.training import jax_loss as l
from rockpool.training.adversarial_jax import adversarial_loss
[2]:
# - Import the required Rockpool modules to build a network
from rockpool.nn.modules import LinearJax, InstantJax
from rockpool.nn.combinators import Sequential
# - Other useful imports
import jax
import jax.numpy as jnp
import jax.tree_util as tu
import jax.random as random
from jax.example_libraries.optimizers import adam, sgd
from jax.tree_util import Partial
from tqdm.autonotebook import tqdm
from copy import deepcopy
from itertools import count
import numpy as np
# - Seed the numpy RNG
np.random.seed(0)
# - Import and configure matplotlib for plotting
import sys
!{sys.executable} -m pip install --quiet matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["figure.figsize"] = [12, 4]
plt.rcParams["figure.dpi"] = 300
Network and training task
We will train a feed-forward network with one hidden layer, to perform a frozen-noise-to-curve regression task. The class below defines a random dataset to use in training.
[3]:
# - Define a dataset class implementing the indexing interface
class MultiClassRandomSinMapping:
def __init__(
self,
num_classes: int = 2,
sample_length: int = 100,
input_channels: int = 50,
target_channels: int = 2,
):
# - Record task parameters
self._num_classes = num_classes
self._sample_length = sample_length
# - Draw random input signals
self._inputs = np.random.randn(num_classes, sample_length, input_channels) + 1.0
# - Draw random sinusoidal target parameters
self._target_phase = np.random.rand(num_classes, 1, target_channels) * 2 * np.pi
self._target_omega = (
np.random.rand(num_classes, 1, target_channels) * sample_length / 50
)
# - Generate target output signals
time_base = np.atleast_2d(np.arange(sample_length) / sample_length).T
self._targets = np.sin(
2 * np.pi * self._target_omega * time_base + self._target_phase
)
def __len__(self):
# - Return the total size of this dataset
return self._num_classes
def __getitem__(self, i):
# - Return the indexed dataset sample
return self._inputs[i], self._targets[i]
# - Define loss for standard network
def loss_mse(parameters, net, inputs, target):
net = net.reset_state()
net = net.set_attributes(parameters)
output, _, _ = net(inputs)
return l.mse(output, target)
[4]:
# - Instantiate a dataset
Nin = 2000
Nout = 2
num_classes = 3
T = 100
ds = MultiClassRandomSinMapping(
num_classes=num_classes, input_channels=Nin, target_channels=Nout, sample_length=T
)
Nhidden = 8
N_train = 100
N_test = 50
data = {
"train": [el for el in [sample for sample in ds] for _ in range(N_train)],
"test": [el for el in [sample for sample in ds] for _ in range(N_test)],
}
[5]:
# Display the dataset classes
plt.figure()
for i, sample in enumerate(ds):
plt.subplot(2, len(ds), i + 1)
plt.imshow(sample[0].T, aspect="auto", origin="lower")
plt.title(f"Input class {i}")
plt.subplot(2, len(ds), i + len(ds) + 1)
plt.plot(sample[1])
plt.xlabel(f"Target class {i}")
The function train_net() below defines a Jax-based training loop, parameterised by the loss functions used to evaluate the task and used by the adversary. This is a farily standard training loop that uses the Adam optimiser. It accepts several parameters for adversarial_loss() and passes them through.
[6]:
# - Create a method that trains a network
def train_net(
net,
loss_vgf,
data,
num_epochs=1000,
task_loss=None,
mismatch_loss=None,
noisy_forward_std=None,
initial_std=None,
mismatch_level=None,
beta_robustness=None,
attack_steps=None,
):
# - Define initial seed
rand_key = random.PRNGKey(0)
# - Get the optimiser functions
init_fun, update_fun, get_params = adam(1e-4)
# - Initialise the optimiser with the initial parameters
params0 = deepcopy(net.parameters())
opt_state = init_fun(params0)
# - Compile the optimiser update function
update_fun = jax.jit(update_fun)
# - Record the loss values over training iterations
loss_t = []
grad_t = []
# - Loop over iterations
i_trial = count()
for _ in tqdm(range(num_epochs)):
for sample in data:
# - Get an input / target sample
input, target = sample[0], sample[1]
# - Get parameters for this iteration
params = get_params(opt_state)
# - Split the random key
rand_key, sub_key = random.split(rand_key)
# - Get the loss value and gradients for this iteration
if mismatch_loss is None:
# - Normal training
loss_val, grads = loss_vgf(params, net, input, target)
else:
loss_val, grads = loss_vgf(
params,
net,
input,
target,
task_loss,
mismatch_loss,
sub_key,
noisy_forward_std,
initial_std,
mismatch_level,
beta_robustness,
attack_steps,
)
# - Update the optimiser
opt_state = update_fun(next(i_trial), grads, opt_state)
# - Keep track of the loss
loss_t.append(loss_val)
return net, loss_t, params
[7]:
# - Define helper functions for evaluating the mismatch robustness of the network
def eval_loss(inputs, target, net):
output, _, _ = net(inputs)
return l.mse(output, target)
def split_and_sample_normal(key, shape):
"""
Split an RNG key and generate random data of a given shape following a standard Gaussian distribution
Args:
key (RNGKey): Array of two ints. A Jax random key
shape (tuple): The shape that the random normal data should have
Returns:
(RNGKey, np.ndarray): Tuple of `(key,data)`. `key` is the new key that can be used in subsequent computations and `data` is the Gaussian data
"""
key, subkey = random.split(key)
val = random.normal(subkey, shape=shape)
return key, val
The function get_average_loss_mismatch() below evaluates the performance of the trained network under simulated mismatch. It performs N simulations of mismatch at level mm_level, based on the trained parameters params, then returns the mean and std. dev. of loss evaluated over dataset.
[8]:
def get_average_loss_mismatch(
dataset, mm_level, N, net, params, rand_key
) -> (float, float):
params_flattened, tree_def_params = tu.tree_flatten(params)
loss = []
# - Perform N simulations of mismatch
for _ in range(N):
# - Simulate mismatch by adding noise to each parameter
params_gaussian_flattened = []
for p in params_flattened:
rand_key, random_normal_var = split_and_sample_normal(rand_key, p.shape)
params_gaussian_flattened.append(
p + jnp.abs(p) * mm_level * random_normal_var
)
params_gaussian = tu.tree_unflatten(tree_def_params, params_gaussian_flattened)
# - Apply the mismatched parameters to the network
net = net.set_attributes(params_gaussian)
# - Evaluate the test data and measure the loss
loss_tmp = []
for sample in dataset:
# - Get an input / target sample
inputs, target = sample[0], sample[1]
net = net.reset_state()
loss_tmp.append(eval_loss(inputs, target, net))
loss.append(np.mean(loss_tmp))
return np.mean(loss), np.std(loss)
Here we define the simple feed-forward network architecture.
[9]:
# - Define number of epochs
num_epochs = 300
# - Create network
net = Sequential(
LinearJax((Nin, Nhidden)),
InstantJax(Nhidden, jnp.tanh),
LinearJax((Nhidden, Nout)),
)
Training the robust network
Now we will train a robust network using the adversarial attack described above, as well as a standard network using the task loss alone.
[10]:
# - Train robust network
loss_vgf = jax.value_and_grad(adversarial_loss)
net_robust, loss_t_robust, params_robust = train_net(
net=deepcopy(net),
loss_vgf=loss_vgf,
data=data["train"],
num_epochs=num_epochs,
task_loss=Partial(l.mse),
mismatch_loss=Partial(l.mse),
noisy_forward_std=0.1,
initial_std=0.001,
mismatch_level=0.025,
beta_robustness=0.25,
attack_steps=10,
)
2022-11-21 16:26:54.131359: W external/org_tensorflow/tensorflow/compiler/xla/service/platform_util.cc:198] unable to create StreamExecutor for CUDA:0: failed initializing StreamExecutor for CUDA device ordinal 0: INTERNAL: failed call to cuDevicePrimaryCtxRetain: CUDA_ERROR_OUT_OF_MEMORY: out of memory; total memory reported: 25431310336
WARNING:jax._src.lib.xla_bridge:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
[11]:
# - Train a standard network
loss_vgf = jax.jit(jax.value_and_grad(loss_mse))
net_standard, loss_t_standard, params_standard = train_net(
net=deepcopy(net), loss_vgf=loss_vgf, data=data["train"], num_epochs=num_epochs
)
Having trained the networks, we will evaluate both robust and standard networks under simulated mismatch.
[12]:
# - Evaluate the robustness of the networks
mismatch_levels = [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6]
results = {
"rob": {
"mean": np.empty(len(mismatch_levels)),
"std": np.empty(len(mismatch_levels)),
},
"standard": {
"mean": np.empty(len(mismatch_levels)),
"std": np.empty(len(mismatch_levels)),
},
}
rand_key = random.PRNGKey(0)
N_rep = 20
for i, mm_level in enumerate(mismatch_levels):
rob_mean, rob_std = get_average_loss_mismatch(
dataset=data["test"],
mm_level=mm_level,
N=N_rep,
net=net_robust,
params=params_robust,
rand_key=rand_key,
)
standard_mean, standard_std = get_average_loss_mismatch(
dataset=data["test"],
mm_level=mm_level,
N=N_rep,
net=net_standard,
params=params_standard,
rand_key=rand_key,
)
rand_key, _ = random.split(rand_key)
results["rob"]["mean"][i] = rob_mean
results["rob"]["std"][i] = rob_std
results["standard"]["mean"][i] = standard_mean
results["standard"]["std"][i] = standard_std
print(f"ROBUST Mismatch level {mm_level} Loss {rob_mean}+-{rob_std}")
print(f"STANDARD Mismatch level {mm_level} Loss {standard_mean}+-{standard_std} \n")
ROBUST Mismatch level 0.0 Loss 0.013262065127491951+-0.0
STANDARD Mismatch level 0.0 Loss 5.5408447224181145e-05+-0.0
ROBUST Mismatch level 0.1 Loss 0.022923123091459274+-0.009204843081533909
STANDARD Mismatch level 0.1 Loss 0.029643213376402855+-0.00973587203770876
ROBUST Mismatch level 0.2 Loss 0.06536121666431427+-0.04339094087481499
STANDARD Mismatch level 0.2 Loss 0.1333199441432953+-0.08620666712522507
ROBUST Mismatch level 0.3 Loss 0.10252754390239716+-0.05598119646310806
STANDARD Mismatch level 0.3 Loss 0.2684288024902344+-0.09571206569671631
ROBUST Mismatch level 0.4 Loss 0.19510497152805328+-0.1397494077682495
STANDARD Mismatch level 0.4 Loss 0.4427710175514221+-0.18473027646541595
ROBUST Mismatch level 0.5 Loss 0.24414198100566864+-0.14068834483623505
STANDARD Mismatch level 0.5 Loss 0.7254256010055542+-0.2870040237903595
ROBUST Mismatch level 0.6 Loss 0.4277869164943695+-0.31552523374557495
STANDARD Mismatch level 0.6 Loss 0.9867719411849976+-0.394449919462204
[13]:
# - Plot the results
x = np.arange(0, len(mismatch_levels), 1)
plt.plot(x, results["rob"]["mean"], color="r", label="Robust")
plt.fill_between(
x,
results["rob"]["mean"] - results["rob"]["std"],
results["rob"]["mean"] + results["rob"]["std"],
alpha=0.1,
color="r",
)
plt.plot(x, results["standard"]["mean"], color="b", label="Standard")
plt.fill_between(
x,
results["standard"]["mean"] - results["standard"]["std"],
results["standard"]["mean"] + results["standard"]["std"],
alpha=0.1,
color="b",
)
plt.gca().set_xticks(x)
plt.gca().set_xticklabels([str(s) for s in mismatch_levels])
plt.gca().set_xlabel(r"$\zeta_{attack}$")
plt.ylabel("MSE")
plt.legend()
plt.show()
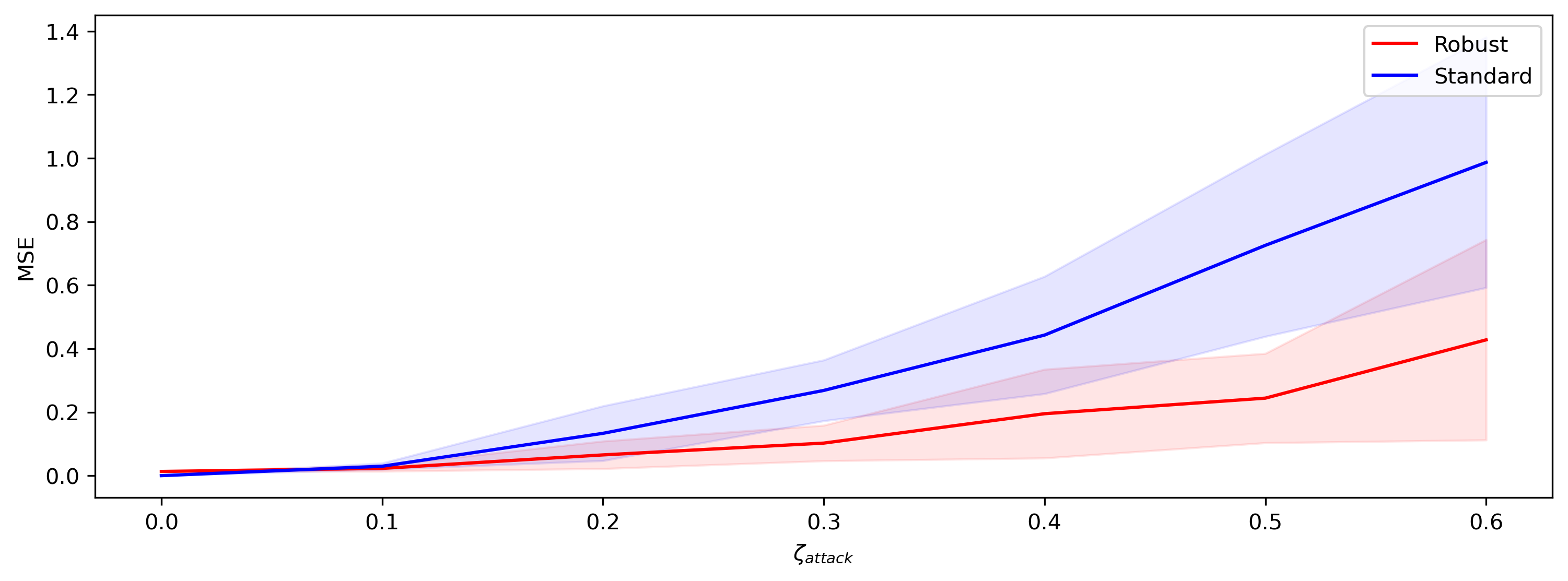
The robust network trained with the adversary performs almost as well as the network with standard training (i.e. low loss for mismatch_level = 0.. At the same time, the robust network is less sensitive to perturbations in the parameters (lower loss for mismatch_level > 0).